指標の算出方法（平均標準距離・平均団地面積など）

本ページでは、米農地集約度分析ダッシュボードにおける各種指標の算出方法について説明します。農地の集約・集積を、平均標準距離や平均団地面積などの指標でどう定量化するかをまとめています。利用時にご留意ください。

← ダッシュボードへ戻る

共通事項

本ダッシュボードはWAGRI API（農研機構）の「統合農地データ」を利用し、当該データを解析することで各種指標を算出しています。なお、統合農地データの圃場情報は全国の農業委員会が整備する農地台帳に基づいており、市町村単位の耕作状況を示しています。
対象としている圃場は以下のとおりです：
- 田を対象としています（ “LandCategoryCode” が「1」）。
- 遊休農地ではない、または調整中の農地を対象に含めています（PinInfo の” IsIdleAgriCulture” が「遊休農地ではない」または「調整中」）。
- 圃場の面積は、統合農地データの面積情報を利用しています。
データの整理方法は以下のとおりです：

同一圃場内に複数の筆が存在する場合は、その中で最大の面積を占める耕作者が耕作しているとみなしています。
圃場の面積は「統合農地データ」の面積情報を利用しています。

現在公表されている2020年農林業センサスとの主な相違点は以下のとおりです（農林水産省 2020）:
- センサスが対象とする農林業経営体は、経営耕地面積が30a以上、または調査期日前1年間の農業生産物の総販売額が50万円相当以上としています。
- センサスでは農林業経営体が居住していない他市町村の耕地も、居住している市町村の経営耕地として集計しています（属人統計）。
総務省「全国地方公共団体コード」（令和6年1月1日更新）に記載されている市区町村のうち、WAGRI APIにデータが存在しないため本ダッシュボードに掲載されていない市町村は、以下の20市区町村となります。
- 北海道：色丹村、泊村（団体コード:16969）、留夜別村、留別村、紗那村、蘂取村
- 千葉県：浦安市
- 東京都：千代田区、中央区、港区、新宿区、文京区、台東区、墨田区、江東区、品川区、渋谷区、豊島区、荒川区
- 静岡県：浜松市

1. 平均耕地面積

耕作者 \(i\) が耕作している圃場 \(j\) の面積を \(a_{i,j}\) 、圃場数を \(m_i\) とすると、耕作者 \(i\) の耕地面積は \(A_i=∑_{j=1}^{m_i} a_{i,j}\)となる。

対象となるエリアおよび階級における耕地面積の「平均」を求める１つめの方法は「耕作者数ベース平均耕地面積」である。これは、\(n\)人の農家が耕作している総耕地面積を、農家数\(n\)で割った算術平均である：

\[ \overline{A}_F = \frac{1}{n} \sum_{i=1}^{n} A_i \]

もう１つの方法は「耕地面積ベース平均耕地面積」である。これは、各耕作者 \(i\) の耕地面積を耕作面積で重みづけたうえで全耕作者について足し合せ、総耕地面積で割った加重平均である。\(n\)人の農家が耕作している総耕地面積を \(A=∑_{i=1}^{n} A_i\) と表記すると：

\[ \overline{A}_W = \frac{1}{A} \sum_{i=1}^n A_i^2 \]

2. 平均圃場数

圃場数についても、\(n\)人の農家が耕作している総圃場数を農家数\(n\)で割った算術平均である「耕作者数ベース平均圃場数」と、各耕作者 \(i\) の圃場数を耕地面積で重みづけたうえで全耕作者について足し合せ、総耕地面積で割った加重平均である「耕地面積ベース平均圃場数」を計算した：

耕作者数ベース平均圃場数：
\[ \overline{M}_F = \frac{1}{n} \sum_{i=1}^{n} m_i \]
耕地面積ベース平均圃場数：
\[ \overline{M}_W =\frac{1}{A} \sum_{i=1}^{n} A_i \cdot m_i \]

3. 平均標準距離

耕作者 \(i\) が耕作している圃場 \(j\) の座標（投影座標系・メートル単位）を \((x_{i,j},y_{i,j})\)、耕作者 \(i\) が耕作している全圃場の平均中心座標を \((\bar{x_i},\bar{y_i})\) 、ただし\(\bar{x_i}= \frac{1}{m_i} ∑_{j=1}^{m_i} x_{i,j},\bar{y_i}=\frac{1}{m_i}∑_{j=1}^{m_i} y_{i, j}\)と表記する。このとき、耕作者 \(i\) の標準距離 \(SD_i\) は次のように定義される（岡村ほか 2021）：

\(SD_i=\sqrt{[\sum_{j=1}^{m_i} \{ (x_{i,j}−\bar{x_i})^2+ (y_{i,j}−\bar{y_i})^2\} ]\frac{1}{m_i}} \)

標準距離についても、\(n\)人の農家の標準距離の合計を農家数\(n\)で割った算術平均である「耕作者数ベース平均標準距離」と、各耕作者 \(i\) の標準距離を耕地面積で重みづけたうえで全耕作者について足し合せ、総耕地面積で割った加重平均である「耕地面積ベース平均標準距離」を計算した：

耕作者数ベース平均標準距離：
\( \overline{SD}_F=\frac{1}{n}\sum_{i=1}^n SD_i\)
耕地面積ベース平均標準距離：
\(\overline{SD}_W=\frac{1}{A}\sum_{i=1}^n A_i \cdot SD_i\)

4. 平均団地数

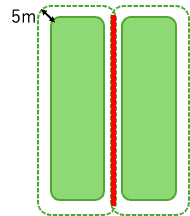
全圃場を外側に5 m広げ、同一の耕作者が耕作する圃場が重なる場合は、それらの圃場を連結して団地とみなした。このようにして求めた各耕作者 \(i\) の団地数を\(p_i\)と表記する。

団地数についても、\(n\)人の農家の団地数の合計を農家数\(n\)で割った算術平均である「耕作者数ベース平均団地数」と、各耕作者 \(i\) の団地数を耕地面積で重みづけたうえで全耕作者について足し合せ、総耕地面積で割った加重平均である「耕地面積ベース平均団地数」を計算した：

耕作者数ベース平均団地数：
\[ \overline{p}_F = \frac{1}{n} \sum_{i=1}^n p_i \]
耕地面積ベース平均団地数：
\[ \overline{p}_W = \frac{1}{A} \sum_{i=1}^n A_i \cdot p_i \]

5. 平均団地面積

各耕作者 \(i\) の平均団地面積\(P_i\) は、耕作者 \(i\) の耕地面積\(A_i=∑_{j=1}^{m_i} a_{i,j}\)を、耕作者 \(i\) の団地数\(p_i\)で割ったものである（岡村ほか 2021）：

\[ P_i = \frac{A_i}{p_i} \]

平均団地面積についても、\(n\)人の農家の団地面積の合計を農家数\(n\)で割った算術平均である「耕作者数ベース平均団地面積」と、各耕作者 \(i\) の団地面積を耕地面積で重みづけたうえで全耕作者について足し合せ、総耕地面積で割った加重平均である「耕地面積ベース平均団地面積」を計算した：

耕作者数ベース平均団地面積：
\[ \overline{P}_F = \frac{1}{n} \sum_{i=1}^n P_i \]
耕地面積ベース平均団地面積：
\[ \overline{P}_W = \frac{1}{A}\sum_{i=1}^n A_i \cdot P_i \]

6. 平均耕地密度

各耕作者 \(i\) について、当該耕作者が耕作する圃場を複数含む「クラスター」を特定する。クラスターの特定方法としてはいくつか考えられるが、本ダッシュボードではHDBSCAN（Campello et al. 2013）を採用する。いま、このようなクラスターが\(K_i\)箇所特定できたとする。

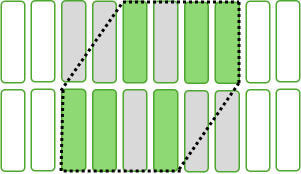
まず、各クラスター\(C_{i,k}\)に含まれる耕作者 \(i\) が耕作する圃場の面積の合計\(A_{i,k}=∑_{a_{i,j}\in C_{i,k}}a_{ij}\)を計算する（緑の面積）。次に、クラスター\(C_{i,k}\)の凸包（クラスターを含む最小の凸集合：点線内部）と一部もしくは全てが含まれる、耕作者 \(i\) を含むすべての耕作者が耕作する圃場の面積の合計\(Conv(C_{i,k})\)を計算する（緑＋灰の面積）。

そのうえで、クラスターの凸包充填率を：

\(FR_{i,k} = \frac{A_{i,k}}{Conv(C_{i,k})}\)

このとき、耕作者 \(i\) の耕地密度を \(\rho_i\) を、各クラスタに含まれる圃場の面積の合計\(A_{i,k}\)を重みとして、\(K_i\)箇所すべてのクラスターについて加重平均した値として定義する：

\(\rho_i = \frac{\sum_{k=1}^{K_i} A_{i,k} \cdot FR_{i,k}}{\sum_{k=1}^{K_i} A_{i,k}}\)

なお、\(∑_{k=1}^{K_i} A_{i,k}=A_i\) であることに注意されたい。

耕作地密度についても、\(n\)人の農家の耕作地占有率の合計を農家数\(n\)で割った算術平均である「耕作者数ベース平均耕作地密度」と、各耕作者 \(i\) の耕作地密度を耕地面積で重みづけたうえで全耕作者について足し合せ、総耕地面積で割った加重平均である「耕地面積ベース平均耕作地密度」を計算した：

耕作者数ベース平均密度：
\[ \overline{\rho}_F = \frac{1}{n} \sum_{i=1}^n \rho_i \]
耕地面積ベース平均密度：
\[ \overline{\rho}_W = \frac{1}{A} \sum_{i=1}^n A_i \cdot \rho_i \]

参考文献

岡村伊織・草苅仁・藤栄剛 (2021)『GISによる広域的な圃場分散状況の把握と農地中間管理事業の評価』農業計画学会論文集, vol. 1, no. 1, pp. 29-39.

農林水産省 (2020)『2020年農林業センサス』https://www.maff.go.jp/j/tokei/census/nougin/2020/index.html

Campello, R.J.G.B., D. Moulavi and J. Sander (2013) "Density-Based Clustering Based on Hierarchical Density Estimates." In Advances in Knowledge Discovery and Data Mining, 7819:pp. 160–72, eds. J. Pei, V.S. Tseng, L. Cao, H. Motoda, and G. Xu. Lecture Notes in Computer Science. Springer.